Todas las proyecciones cartográficas producen deformaciones dado que se trata de representar en un plano una superficie esférica y por esta razón se las clasifica en por lo menos tres grupos: conformes, equivalentes y equidistantes.
Gauss – Krüger, y su caso particular UTM, son conformes, es decir que conservan las formas o, en otras palabras, los ángulos en la superficie terrestre son iguales a los que se representan en la carta. El cálculo directo de los mismos parecería negar esta igualdad, sin embargo teniendo presente la corrección arco-cuerda (o reducción de acimut o t-T) la condición se cumple.
En Gauss – Krüger
Las distancias, por su parte, tienen una deformación lineal llamada “m” que resulta del cociente entre la distancia en el plano y su homóloga en la superficie del elipsoide. El cálculo de “m” se puede obtener para cada punto mediante la expresión
R, el radio medio terrestre en el punto de interés
Cuando se trata de obtener la deformación de una distancia entre dos puntos se suele determinar el valor de “m” como promedio entre los extremos de la línea en cuestión. Una mejor solución para su cálculo se alcanza aplicando la siguiente fórmula publicada por Ordnance Survey of Ireland
Para el cálculo de las superficies a partir de las coordenadas planas se suele apelar a una proyección equivalente, sin embargo es también posible obtenerla a partir de las coordenadas planas Gauss – Krüger en cuyo caso se calcula el valor de m para el centro del área y, elevado al cuadrado, es el divisor del valor de la superficie obtenida. El error que se produce es poco significativo.
En UTM
El valor de m anterior se lo multiplica por k = 0,9996 o sea que
Nota: Texto escrito por el Agrim. Rubén C. Rodríguez.


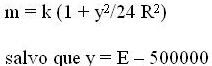
En Gauss Kruguer esta claro que la sección del cilindro tangente al elipsoide es una elipse con dimensiones i forma análogas al elipsoide. Pero en UTM dado el artificio de Tissot, ¿Podríamos decir que la sección del cilindro secante al elipsoide es otra elipse de semieje mayor de menor dimensión pero que contiene a los polos? O sea una elipse cuyo cuarto de meridiano es 0.9996 veces sl meridiano del elipsoide considerado. ¿Cómo podríamos expresarlo de forma sencilla y clara?
ResponderEliminarEfectivamente, en UTM se trata también de un cilindro pero en este caso secante en lugar del tangente de Gauss – Krüger.
EliminarEl número k = 0.9996 es por la reducción entre tangente y secante que afecta a las coordenadas X (Norting en UTM) e Y (Easting en UTM) en las expresiones:
N = Q + k x (en el hemisferio Sur, Q es cuadrante = 10 000 000 cualquiera sea el elipsoide)
E = 500 000 + k y
x e y son las mismas expresiones de Gauss – Krüger donde Q depende del elipsoide y arranca en el Polo Sur, mientras que en UTM el origen está a 10000000 metros del Ecuador.
Z, zona (de 1 a 60)
Las figuras que aparecen en https://www.uwgb.edu/dutchs/FieldMethods/UTMSystem.htm ayudan a comprender la situación.
Rubén Rodríguez
Parece que quedo mal el modulo de deformacion lineal. Deberaia ser 1+y2/2R2+y4/24R4+...
ResponderEliminar